【Blog】使用Typescript描述原群、半群、幺半群

"我个人对于 PKU 今年暑期的 PL 课程 Functional Programming with Abstact Algebra 的学习笔记，里面简单地使用 Typescript 描述了原群、半群、幺半群等代数结构。"

虽然标题说是 Blog，这其实可以算作是我个人对于 PKU 今年暑期的 PL 课程 Functional Programming with Abstact Algebra 的学习笔记。

在抽象的海洋里徜徉，总是会让人不禁畏惧水下的深渊。

我也不知道自己是第几次重新碰触抽象的数学概念了。它真的是让人着迷。

关于这部分的实现代码，可见：https://github.com/WendaoLee/FPWithAbstractAlgebra

在开始之前... From The Void

在编程的范式上，基本上可以分为两大类：面向对象式编程和函数式编程。

面向对象是一个不错的思想。它把编程的目标事物理解为一个个拥有行为的对象，通过对象之间的交互去建模整个世界。然而面向对象式的编程过多地依赖于类这个概念，从而导致代码的杂糅与耦合，以至于大家总爱在类上弄杂七杂八的设计模式以解决这个问题。

是的，这一点同样可以通过合理的领域建模去规避，但是我讨厌写一堆又一堆的 class ，在 class 之间不知道要 extends 多少层。面向对象的思想虽然简单，但是它多少忽略了编程的计算本质。

所以在三年前我开始接触函数式编程，也就是所谓的 FP。我喜欢函数式的思想，它把万事万物都看作是输入输出的过程，我只需要依靠函数以及类型的变化去理解事物，我可以借用数学上的概念对事物进行建模，还能对我写的东西在形式上进行推演证明。只能说，抽象是一种让人无法拒绝的甜美毒酒，尽管我知道在抽象事物时总是不自觉地就过度抽象了，而过度的抽象实际上不利于帮助他人理解，但那种将世界提炼成一个个符号的诱惑总是让我情不自禁地端起眼前满溢的酒杯，将甜蜜与荼毒一饮而尽。

然而 FP 是一个大坑，总感觉你没学懂范畴论、类型论、计算理论、同调代数、抽象代数等等东西都不敢说自己懂 FP，况且我并不是一个聪明人，加上现实世界总不如理想那般容易建模。于是我磕磕绊绊半吊子地学了两年，好吧，虽然说现在的我能写出一手自己过个几年还能读懂的代码，但依然不敢说自己懂 FP ，然后我又染上了狗屎的抽象瘾，不管怎样忙，不隔一段时间玩玩抽象的东西浑身难受。

于是，你就看到了这篇文章。这是我抽象瘾上来+刚好 PKU 今年的PL课是我感兴趣的方向于是我就去看了看的产物。权当是给自己回顾一下过去接触的各种抽象概念。我尝试使用 Typescript 描述这门课里提到的各种概念，代码可见 https://github.com/WendaoLee/FPWithAbstractAlgebra 。

关于这门课的核心观点，你可以用下面这张图去理解：

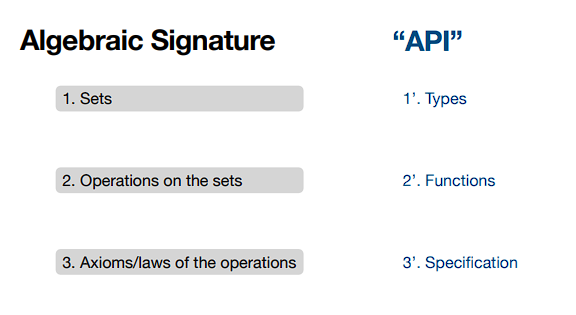
即，代数结构通常由这三部分组成：

由构成该代数结构的元素组成的集合
定义在集合上的操作
以及操作应该满足的定律与规则

而组成代数结构的这三者可以美妙地和编程语言中的API一一对应：

集合对应于类型
集合上的操作对应于在类型之间进行变换的函数，即相应API的具体操作
操作满足的定律和规则对应于使用这些函数的规范

因此，我们可以尝试通过代数结构去组建编程里的各类API。

下面是一些基本代数结构的阐述与实现。

原群，封闭的原群~

在开始之前，我觉得可能举几个例子会比较好。

通常，对于一个代数结构，我们会这样称呼它：“一个< 什么集合 >< 具有什么操作 >的< 代数结构 >”，例如，一个 “整数加法群”，表示它是一个建立在整数集上、附带加法操作的群结构；一个 “自然数乘法半群”，表示它是一个建立在自然数集上、附带乘法操作的半群结构。

我们有时会用 <> 与 , 去符号化描述一个代数结构。例如 <Z,+> 可以用于表示一个整数加法半群；<Z,+,0> 可以用于表示一个整数加法幺半群。

对于上面的例子里提到的代数结构，会在下面进行定义与阐述。

好了，现在，让我们正式接触代数结构。先从一个最基础的代数结构原群（Magma）说起。

前面讲过，代数结构由这三部分组成：

由构成该代数结构的元素组成的集合
定义在集合上的操作
以及操作应该满足的定律与规则

那么，原群按定义为：

存在一个集合M
在集合M上存在一个二元操作⊕ ，使得对于集合M中的任意元素进行操作，得到的结果也属于M，即: M ⊕ M -> M 。这一点也是代数结构所具备的封闭性：组成代数结构的集合与操作永远都在该代数结构中。
原群不存在额外的定律与规则。

原群是最为基础的代数结构，它可以这样表示 <M,⊕> 。

相应的 Typescript 描述如下：

/**
 * @inspiredBy fp-ts
 * 原群 (Magma) :=
 * 1. 存在一个集合 M
 * 2. 在集合 M 上定义了一个二元运算 ⊕ ，使得 ⊕:M x M -> M ,即对于任意 a, b ∈ S ，都有 a * b ∈ S，即具有封闭性的二元运算
 * 根据对应集合的不同，操作的实现可能会有所不同
 */
export interface Magma<M> {
    /**
     * 二元运算, ⊕ ，它可以是 加法、乘法、减法等
	 * 如你所见，原群上的二元操作的输入与输出都在原群集合的范围内。满足了封闭性。
     * @param a 
     * @param b 
     * @returns 
     */
    biOperation: (a: M, b: M) => M;
}

通过具体指定原群的集合和相应的二元操作，我们能够得到许多我们熟知的事物。

例如说，实数集和实数集上的加法共同构成了一个实数加法群 <R,+> ：

/**
 * @inspiredBy fp-ts/number.ts
 * @note 由于 TypeScript 不存在 Int ，所以无法定义 PPT 上的 Int原群
 * 由于 Typescript 没有实数、整数的概念，因此我们以数值代替
 * 一个 数值加法原群 <Number,+>
 */
export const MagmaNumberWithAddition: Magma<number> = {
    biOperation: (a: number, b: number): number => a + b
}

实数集和实数集上的减法共同构成了一个实数减法群：

/**
 * 一个 数值减法原群 <Number,->
 */
export const MagmaNumberWithSubtraction: Magma<number> = {
    biOperation: (a: number, b: number): number => a - b
}

原群，或者说代数结构的重要意义在于它的封闭性，如果一种数据结构和它的操作能够构成一个原群，那么它的操作结果永远封闭在原群上，而不会跑到其他地方——这也是数学以及形式化的魅力，我们精确化了一样事物，消除了不确定性。不确定性总是让人厌恶的。

以我们熟知的数据结构全二叉树（指不存在只有一个子节点的节点的二叉树）为例，在 TypeScript 中，它可以这样定义：

/**
 * 全二叉树的定义
 * 它相当于 Haskell 中的
 * data Tree a = Leaf a | Fork (Tree a) (Tree a)
 * 
 * 也是 代数数据结构（ADT） 中的积类型。
 */
export type FullBinaryTree<M> = Leaf<M> | Fork<M>
 
/**
 * 关于这种表达方式
 * @see https://www.typescriptlang.org/docs/handbook/typescript-in-5-minutes-func.html#discriminated-unions
 */
interface Leaf<M> {
    kind: 'Leaf'
    value: M
}
 
interface Fork<M> {
    kind: 'Fork'
    left: FullBinaryTree<M>
    right: FullBinaryTree<M>
}
 
const sampleNumberTree: FullBinaryTree<number> = {
    kind: 'Fork',
    left: {
        kind: 'Leaf',
        value: 1
    },
    right: {
        kind: 'Fork',
        left: {
            kind: 'Leaf',
            value: 2
        },
        right: {
            kind: 'Leaf',
            value: 3
        }
    }
}

这样写可能有点抽象，用一张图表示我们定义的 sampleNumberTree 是这样：

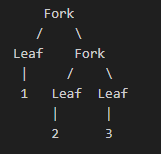
我们可以说一个数值全二叉树（树的节点值为 number）以及它的合并（此处称之为 fork ）操作构成了一个原群 <FullBinaryTree<number>,fork> :

/**
 * 全二叉树带 Fork 操作的原群
 */
export const MagmaFullBinaryTreeWithFork: Magma<FullBinaryTree<number>> = {
    /**
     * 操作 fork ，将两个二叉树合并为一个新的二叉树
     * @param a 
     * @param b 
     * @returns 
     */
    biOperation: (a: FullBinaryTree<number>, b: FullBinaryTree<number>): FullBinaryTree<number> => ({
        kind: 'Fork',
        left: a,
        right: b
    })
}

好吧，原群之间，亦有变换

在上面的文本中，我们只讲述了原群和一个原群自身的操作，事实上，不同的原群之间也是存在转换（或者说映射）的。

例如，一个实数加法原群 <R,+> 可以通过一个指数函数 $f(x)=e^x;f:R\rightarrow R$ 映射到一个实数乘法原群 <R,*> 上：

$f(x+y)=e^{x+y}=e^xe^y=f(x)*f(y)$ $f(1+2)=e^{1+2}=e^3=e*e^2=f(1)*f(2)$

数学上，我们管代数结构之间的这种映射（转换，我个人更喜欢说映射）称之为 态射（Morphism）。其中，如果两个代数结构在经过这种映射后能够保持原有的结构，那么我们称之为 同态态射（Homomorphism）。

同态态射的定义是，对于代数结构 $< M_1,\oplus_1 >$ 与 $< M_2,\text{⊕}_2 >$ ，如果有映射 $h:M_1 \rightarrow M_2$ 使得对于 $M_1$ 中的任意元素 $x,y$ ，都能满足 $h(x \text{⊕}_1 y) = h(x)\text{⊕}_2h(y)$ ，那么则称 h 为代数结构 $< M_1,\text{⊕}_1 >$ 与 $< M_2,\text{⊕}_2 >$ 的同态态射，因为 h 维持了相应代数结构的操作。

用一张草图说明也许会好一些（画得比较丑，凑合一下）：

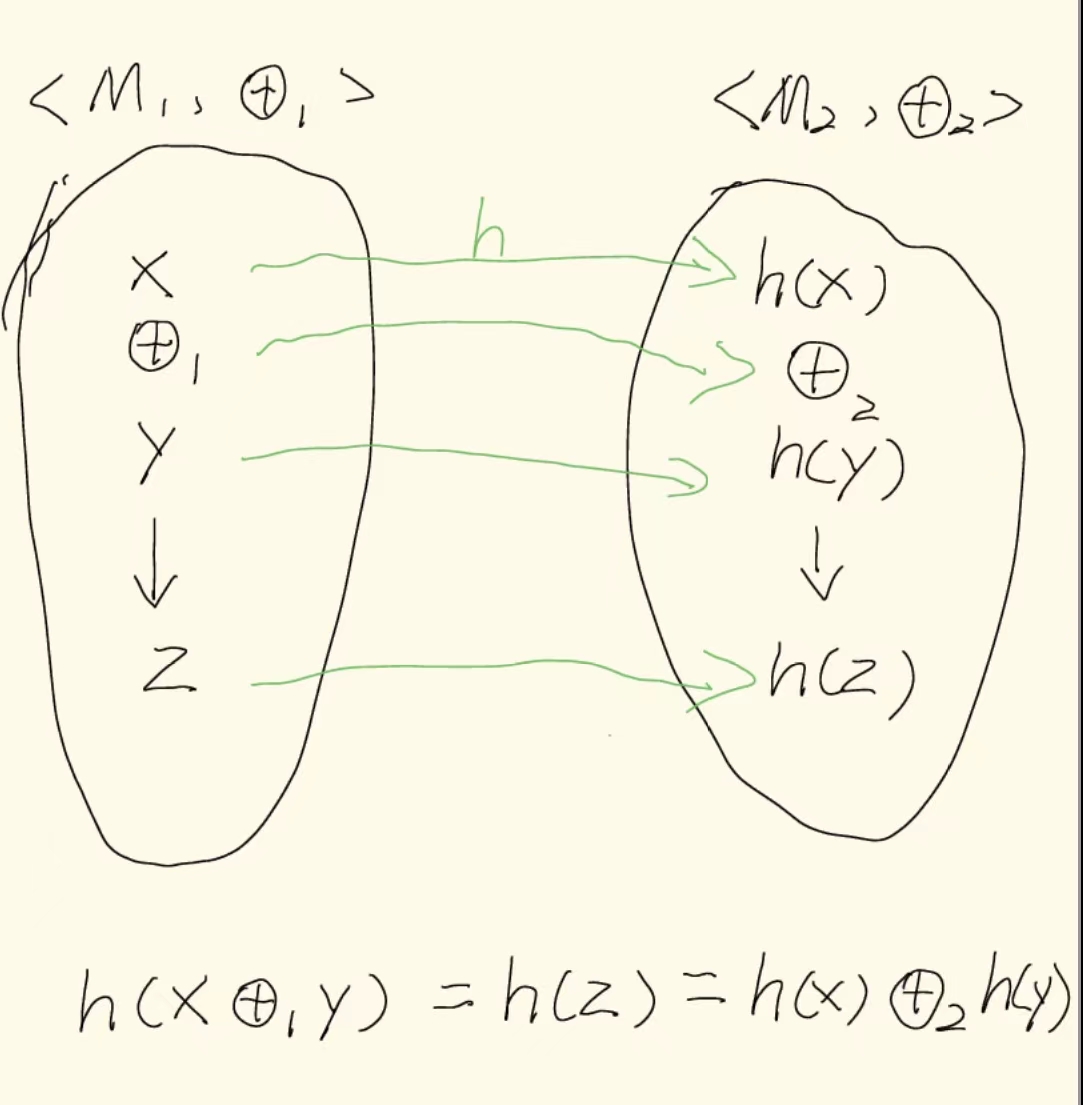
上面的指数函数便是实数加法原群与实数乘法原群之间的同态态射，因为 $f(x+y)=e^{x+y}=e^xe^y=f(x)*f(y)$ 。

回到我们的数值二叉树合并操作原群，我们可以找到它和其他原群之间的态射。例如，我们可以把二叉树的所有节点的值进行求和运算 tsum ，此时，tsum 便是数值二叉树原群与数值原群之间的态射：

/**
 * tsum :: FullBinaryTree Number -> Number
 * 实质上是一个在 <Tree Number,⊕> 和 <Number,⊕>之间的同态态射
 * 这就是同态态射，在不同的代数结构之间保持彼此结构完整性的变换。
 */
type tsum = (a: FullBinaryTree<number>) => number
export const tsum: tsum = (a: FullBinaryTree<number>): number => {
    return match(a)
        /**
         * tsum (Leaf n) = n
         */
        .with({ kind: 'Leaf' }, ({ value }) => value)
        /**
         * tsum (Fork left right) = tsum left + tsum right
         */
        .with({ kind: 'Fork' }, ({ left, right }) => tsum(left) + tsum(right))
        .run()
}

半群，满足结合律的原群

原群是基础的代数结构，从它出发，通过补充不同的性质，我们可以构造出不同的满足群结构的代数结构。例如说 半群（Semigroup）。

让我们回到代数结构的定义组成：

由构成该代数结构的元素组成的集合
定义在集合上的操作
以及操作应该满足的定律与规则

因此，半群的定义为：

存在一个集合M
在集合M上存在一个二元操作⊕ ，使得对于集合M中的任意元素进行操作，得到的结果也属于M，即: M ⊕ M -> M 。这一点也是代数结构所具备的封闭性：组成代数结构的集合与操作永远都在该代数结构中。
集合M与相应的二元操作应该满足结合律（associativity），即对于任意 a, b, c ∈ M ，都有 (a ⊕ b) ⊕ c = a ⊕ (b ⊕ c)

使用 Typescript 可以这样通过原群定义一个半群：

/**
 * 半群 (Semigroup) :=
 * 1. 存在一个集合 M
 * 2. 在集合 M 上定义了一个二元运算 ⊕ ，使得 ⊕:M x M -> M ,即对于任意 a, b ∈ S ，都有 a * b ∈ S，即具有封闭性的二元运算
 * 3. 满足结合律，即对于任意 a, b, c ∈ M ，都有 (a ⊕ b) ⊕ c = a ⊕ (b ⊕ c)
 * 半群 (Semigroup) 是原群，在满足原群的性质上，它还满足结合律
 */
export interface Semigroup<M> extends Magma<M> {
    /**
     * 半群应该满足结合结合律
     * 即 ∀ a, b, c ∈ M, (a ⊕ b) ⊕ c = a ⊕ (b ⊕ c)
     * 很可惜 TypeScript 没有办法表达这个性质，所以这里只能用注释和一个使用起来没意义的类型注释进行诠释
     * @param a 
     * @param b 
     * @param operation 半群自带的二元运算操作
     * @returns 
     */
    associative: (a: M, b: M, biOperation: (arg0: M, arg1: M) => M) => boolean
}

例如说，数值和加法共同构成了一个数值加法半群 <number,+> ，因为 1 + (2 + 3) = (1 + 2) + 3 ：

/**
 * 数值加法半群
 */
export const SemigroupNumberWithAddition: Semigroup<number> = {
    biOperation: (a: number, b: number): number => a + b,
    associative(a, b, biOperation) {
        return biOperation(biOperation(a, b), b) === biOperation(a, biOperation(b, a))
    },
}

代数结构的组成集合并不局限于单种数值，一个定义域与值域一致的函数——我们称之为自函数（endofunction）—— 也可以通过组合（composition，或者说复合，即将两个函数组合在一起的操作，数学上通常以 . 表示。函数想要复合在一起，要求其中一个函数的输出是另外一个函数的输入）也可以构成一个自函数组合半群 <f, . > ：

/**
 * 自函数 Endofunction
 */
type Endofunction<A> = (a: A) => A
 
/**
 * 一个返回自身的数值自函数
 * 这种自函数也叫做 恒等函数 (identity function)
 * f:number -> number
 */
export const identityNumberEndofunction: Endofunction<number> = (a: number) => a
 
/**
 * 自函数组合（或者说 复合）半群，
 * 此时，半群的集合是自函数的集合，半群的操作是函数的复合
 */
export const SemigroupNumberEndofunctionWithComposition: Semigroup<Endofunction<number>> = {
    biOperation: (f: Endofunction<number>, g: Endofunction<number>): Endofunction<number> => (a: number) => f(g(a)),
    associative(a, b, biOperation) {
        return biOperation(biOperation(a, b), b) === biOperation(a, biOperation(b, a))
    }
}

有一些在大多数过程式的编程语言中少见、但在函数式的编程语言中常见的数据结构可被认为是半群，例如非空列表：

/**
 * 非空列表 
 * data NEList a = Nil a | Cons a (NEList a)
 * Nil 指示对应的元素是列表的末尾
 */
type NEList<a> = Nil<a> | Cons<a>
 
interface Nil<a> {
    kind: 'Nil',
    value: a
}
 
interface Cons<a> {
    kind: 'Cons',
    head: a,
    tail: NEList<a>
}
 
const sampleNEList: NEList<number> = {
    kind: 'Cons',
    head: 1,
    tail: {
        kind: 'Cons',
        head: 2,
        tail: {
            kind: 'Nil',
            value: 3
        }
    }
}
 
 
/**
 * 非空列表的连接操作
 * 此处改写为 Haskell 代码，为：
 * instance Semigroup (NEList a) where 
 *        Nil x     <> ys = Cons x ys 
 *        Cons x xs <> ys = Cons x (xs <> ys)
 * 上面的 <> 便是此处的 contact
 * @param pre 
 * @param next 
 * @returns 
 */
const contact = <a>(pre: NEList<a>, next: NEList<a>): NEList<a> => {
    return match(pre)
        .with({ kind: 'Nil' }, ({ value }) => {
            return {
                kind: 'Cons',
                head: value,
                tail: next
            }
        })
        .with({ kind: 'Cons' }, ({ head, tail }) => {
            return {
                kind: 'Cons',
                head: head,
                tail: contact(tail, next)
            }
        }).run() as NEList<a>
}
 
/**
 * 非空数值列表的连接操作半群
 * (Number,contact)
 */
export const SemigroupNumberNEListWithContact: Semigroup<NEList<number>> = {
    /**
     * 非空列表之间可以进行 连接 操作
     * @param nil 
     * @param cons 
     * @returns 
     */
    biOperation: contact,
    associative(a, b, operation) {
        return operation(operation(a, b), b) === operation(a, operation(b, a))
    }    
}

和原群一样，它也存在到其它半群上的同态态射：

/**
 * nesum :: NEList Int -> Int
 * 一个在 (NEList Int,contact) 和 (Int,+) 之间的同态态射（homomorphism）
 * 同态态射是在代数结构之间保持结构的映射
 * e.g. (A,·),(B,*) 如果它们存在同态态射 f:A->B, 那么对于任意 a,b ∈ A, f(a·b) = f(a) * f(b)
 */
type nesum = (a: NEList<number>) => number
export const nesum: nesum = (a: NEList<number>): number => {
    return match(a)
        .with({ kind: 'Nil' }, ({ value }) => value)
        .with({ kind: 'Cons' }, ({ head, tail }) => head + nesum(tail))
        .run()
}

在前面，我们只讲了代数结构之间存在着的互相作用。实际上，代数结构同样也可以作用在普通的集合上，即使该集合并不像代数结构那般存在操作的定义，此时，代数结构的作用便可视为该集合的对象存在的行为。

例如，向量的旋转便可以视为一个实数加法半群从左边作用（Action）在向量集合上：

例如，实数集的幂等可被视为一个自然乘法半群从右边作用于实数集上：

这两个例子径直来自于Tom Schrijvers在PKU的课程的Slides ^[1]。它的意义在于提供了一种视角，即我们可以把对象的行为看作是一种代数结构对某个集合的作用。

根据半群在运算位置的左右，我们可以称这种半群对集合的作用为半群的左作用（Left Semigroup Action）或右作用（Right Semigroup Action）。两者的区别在于运算位置的不同，实质上是差不多的东西。

对于半群的作用的 Typescript 实现如下：

/**
 * Left Semigroup Action,左半群作用，或者说半群从左边作用。用于展示半群元素如何作用于集合元素
 * 代数结构的作用的意义在于，它提供了一种视角，让我们可以把集合中的对象具有的行为看作是某种代数结构作用于集合的元素上。
 * 其中，M 代表半群，S 代表集合
 * ∙ : M × S → S
 * (x ⊕ y) ∙ s = x ∙ (y ∙ s)
 * 
 * 在这里，由于 Typescript 不存在 Semigroup => M 这样的对类型的约束，而实际上的运算是使用 Semigroup 中的成员，因此此处定义实际上并不精确
 * 合理的定义应该是 LeftSemigroupOperation<Semigroup => M, S> = (m:M, s: S) => S
 */
export type LeftSemigroupAction<M, S> = (m:M, s: S) => S
 
 
/**
 * Vector 定义
 */
export type Vector = {
    x:number,
    y:number
}
 
/**
 * 向量的旋转是一个左半群作用, 旋转角度是一个数值加法半群
 * @param m 数值半群
 * @param s 
 * @returns 
 */
export const vectorRotation: LeftSemigroupAction<number, Vector> = (m, s) => {
    // 计算旋转角度
    const radians = (m * Math.PI) / 180
    return {
        // 避免精度以及-0的问题
        x:parseFloat((Math.cos(radians) * s.x - Math.sin(radians) * s.y).toFixed(2)) === -0?0:parseFloat((Math.cos(radians) * s.x - Math.sin(radians) * s.y).toFixed(2)),
        y:parseFloat((Math.sin(radians) * s.x + Math.cos(radians) * s.y).toFixed(2)) === -0?0:parseFloat((Math.sin(radians) * s.x + Math.cos(radians) * s.y).toFixed(2))
    }
}
 
export const sampleVector = {x:1, y:0}
 
 
/**
 * 对于JS中的对象，我们可以使用 JSON.stringify 来判断两个对象是否相等
 * 否则会因为是引用比较，而导致无法得出正确结果
 * @param a 
 * @param b 
 * @returns 
 */
export const equal = (a:Object, b:Object) => JSON.stringify(a) === JSON.stringify(b)
 
/**
 * 此处 ∙ 代表左半群作用
 * 满足结合律
 * (30 + 60) ∙ sampleVector = 30 ∙ (60 ∙ sampleVector)
 */
export const sampleLeftSemigroupOperationOfVectorRoation = (
    equal(
        vectorRotation((30 + 60), sampleVector),
        vectorRotation(30, vectorRotation(60, sampleVector))
    )
)
 
/**
 * Right Semigroup Action,右半群作用。用于展示半群元素如何作用于集合元素
 * 其中，M 代表半群，S 代表集合
 * ∙ : S × M → S
 */
export type RightSemigroupAction<S, M> = (s: S, m: M) => S
 
/**
 * 幂等是一个右半群作用，幂等元素 N 是一个乘法半群，它作用在实数集上。
 * ^ : R x N -> R
 */
export const N:Semigroup<number> = {
    biOperation: (a, b) => a ** b,
    associative(a, b, operation) {
        return operation(operation(a, b), b) === operation(a, operation(b, a))
    }
}
export const power: RightSemigroupAction<number, number> = (s, m) => s ** m
export const sampleRightSemigroupOperationOfPower = (
    power(2,(3*2)) === power(power(2,3),2)
)

如果你审慎地思考一下，会发现我们甚至可以把半群的作用看作是一个到自函数复合半群上的同态态射，你会发现它同时是一种 Curry：

/**
 * 左半群作用和右半群作用实质上共同体现了半群的 结合性。
 * 
 * 对于左半群作用和右半群作用（统称为 Action）:
 * · : M x S -> S
 * 
 * 实质上可以理解为使用一个 半群元素 和 一个集合元素 经过 Action 之后得到一个新的集合元素，即一个 M -> S -> S 的映射。
 * 于是，我们可以这么理解 Action：M -> (S -> S)
 * 
 * 而 (S -> S, ∘) 又是一个半群，其中 ∘ 代表函数的复合。数学上称之为自同态群。
 * 
 * 故而，我们可以认为 Action 是一个到 (S -> S, ∘) 的同态态射，即 M -> (S -> S)。
 * 这也就是所谓的 currying
 */

神奇吧？

幺半群，满足恒等律且具有幺元的半群

现在，让我们简单地回顾一下我们的内容。

我们首先定义了原群，它是一个携带二元运算的集合，它不存在任何性质；而后，我们在原群的基础上为它添加规则上的定义，我们规定它的二元运算应该满足结合律，于是我们定义出了半群。

现在，和定义半群类似，通过给半群添加一个名为单位元（也称幺元，“幺”音“腰”），并且添加恒等律，我们可以定义出幺半群：

幺半群存在一个集合M
幺半群在集合M上存在一个二元操作⊕ ，使得对于集合M中的任意元素进行操作，得到的结果也属于M，即: M ⊕ M -> M 。
对于幺半群的集合M与相应的二元操作，它们应该满足结合律，即对于任意 a, b, c ∈ M ，都有 (a ⊕ b) ⊕ c = a ⊕ (b ⊕ c)。即满足结合律。
在幺半群的集合M中，存在一个单位元 ɛ，使得对于任意集合M中的元素 a，a 与 ɛ 之间的二元操作 ⊕ 永远返回 a 自身，即 ɛ ⊕ a = a = a ⊕ ɛ 。这一性质我们称之为恒等律（identity）。

也许你有些迷糊，但是我们简单举几个例子就很好理解了：

一个整数加法群为一个幺半群，此时幺元为整数0，因为 0 + 2 = 2 = 2 + 0。
一个整数乘法群为一个幺半群，此时幺元为整数1，因为 1 x 2 = 2 = 2 x 1。
一个布尔和群为一个幺半群，此时幺元为 true (或者说 1)，因为 1 && 1 = 1 = 1 && 1 ，1 && 0 = 0 = 0 && 1

幺半群只是多了一个单位元，如此而已~

幺半群可以这样子通过 Typescript 进行定义，现在大家应该熟悉了这些代码，因此下面的代码我附带了相关的示例实现：

/**
 * @inspiredBy fp-ts/Monoid.ts
 * 
 * 幺半群 (Monoid) :=
 * 1. 存在一个集合 M
 * 2. 在集合 M 上定义了一个二元运算 ⊕ ，使得 ⊕:M x M -> M ,即对于任意 a, b ∈ S ，都有 a * b ∈ S，即具有封闭性的二元运算
 * 3. 满足恒等律，即存在一个单位元 ɛ ∈ M ，使得对于任意 a ∈ M ，都有 ɛ ⊕ a = a = a ⊕ ɛ 。
 *    恒等律即集合中的任何元素与单位元进行运算，都会得到原来的元素。
 *    同样，也可认为 ɛ 是一种操作。
 * 4. 满足结合律
 * 
 * 即，幺半群 = 半群 + 单位元
 */
export interface Monoid<M> extends Semigroup<M> {
    /**
     * 单位元，也可称之为幺元、零元
     */
    readonly empty: M
    /**
     * 恒等律
     * 同样，由于 TypeScript 的限制，这里只能用注释和没什么卵用的声明来表达这个性质
     * @returns 
     */
    identity: (empty: M, ele: M, operation: (arg0: M, arg1: M) => M) => boolean
}
 
/**
 * 布尔和 幺半群
 * (Boolean,&&,true)
 * 此时的 ⊕ 为 逻辑与 ，单位元为 true (布尔代数可用⊤表示)
 */
export const MonoidBooleanWithConjunction: Monoid<boolean> = {
    biOperation: (a: boolean, b: boolean): boolean => a && b,
    associative(a, b, operation) {
        return operation(operation(a, b), b) === operation(a, operation(b, a))
    },
    empty: true,
    /**
     * true && true = true = true && true
     * true && false = false = false && true 
     */
    identity(empty, ele, operation) {
        return operation(empty, ele) === ele
    }
}
 
/**
 * 布尔或 幺半群
 * (Boolean,||,false)
 * 此时的 ⊕ 为 逻辑或 ，单位元为 false (布尔代数可用⊥表示)
 */
export const MonoidBooleanWithDisjunction: Monoid<boolean> = {
    biOperation: (a: boolean, b: boolean): boolean => a || b,
    associative(a, b, operation) {
        return operation(operation(a, b), b) === operation(a, operation(b, a))
    },
    empty: false,
    /**
     * false || true = true = true || false
     * false || false = false = false || false
     */
    identity(empty, ele, operation) {
        return operation(empty, ele) === ele
    }
}
 
/**
 * 数值加法 幺半群
 * (Number,+,0)
 * 此时的 ⊕ 为 加法 ，单位元为 0
 */
export const MonoidNumberWithAddition: Monoid<number> = {
    biOperation: (a: number, b: number): number => a + b,
    associative(a, b, operation) {
        return operation(operation(a, b), b) === operation(a, operation(b, a))
    },
    empty: 0,
    /**
     * 0 + 1 = 1 = 1 + 0
     * 0 + 0 = 0 = 0 + 0
     */
    identity(empty, ele, operation) {
        return operation(empty, ele) === ele
    }
}
 
/**
 * 数值乘法 幺半群
 * (Number,*,1)
 * 此时的 ⊕ 为 乘法 ，单位元为 1
 */
export const MonoidNumberWithMultiplication: Monoid<number> = {
    biOperation: (a: number, b: number): number => a * b,
    associative(a, b, operation) {
        return operation(operation(a, b), b) === operation(a, operation(b, a))
    },
    empty: 1,
    /**
     * 1 * 2 = 2 = 2 * 1
     * 1 * 1 = 1 = 1 * 1
     */
    identity(empty, ele, operation) {
        return operation(empty, ele) === ele
    }
}
 
/**
 * 自函数Endofunction
 */
type Endofunction = <A>(a: A) => A
 
/**
 * 自函数组合 幺半群
 * 此时， ⊕ 为 函数组合(或称复合) ，单位元为永远返回自身的函数
 */
export const MonoidEndofunctionWithComposition: Monoid<Endofunction> = {
    biOperation: (f: Endofunction, g: Endofunction): Endofunction => (a: any) => f(g(a)),
    associative(a, b, operation) {
        return operation(operation(a, b), b) === operation(a, operation(b, a))
    },
    /**
     * 返回自身的函数即为 自函数组合幺半群 的单位元
     * @param a 
     * @returns 
     */
    empty: (a: any) => a,
    /**
     * f . id = f = id . f
     */
    identity(empty, ele, operation) {
        return operation(empty, ele) === ele
    }
}

编程语言中的数组（有的地方称之为列表），实际上便是一个幺半群。因为数组可以视为空数组 [] 与非空数组之间的结合，例如 [1,3] := [1] ++ [3] ++ [] ，我们可认为数组是一个单位元为 [] 的幺半群：

/**
 * 因为 TS 的数组便是列表，因此这里直接使用 Array 了~
 */
type List<a> = Array<a>
 
/**
 * 数值列表及其连接操作构成了一个半群
 * (List Number,concat)
 */
export const SemigroupListWithConcatenation: Semigroup<List<number>> = {
    /**
     * 列表的连接操作即为其上的二元运算
     * @param a 
     * @param b 
     * @returns 
     */
    biOperation: (a: List<number>, b: List<number>): List<number> => a.concat(b),
    associative(a, b, operation) {
        return operation(operation(a, b), b) === operation(a, operation(b, a))
    }
}
 
/**
 * 数值列表、连接操作及空列表构成了一个幺半群
 * (List Number,concat,[])
 * 由于该幺半群是基于 Number 幺半群生成的，因此也称之为 自由幺半群（Free Monoid）
 * 此时， ⊕ 为 列表连接 ，单位元为 空列表 []
 */
export const MonoidListWithConcatenation: Monoid<List<number>> = {
    biOperation: (a: List<number>, b: List<number>): List<number> => a.concat(b),
    associative(a, b, operation) {
        return operation(operation(a, b), b) === operation(a, operation(b, a))
    },
    /**
     * 空列表即为 数值列表的幺半群 的单位元
     */
    empty: [],
    /**
     * [] + [1,2,3] = [1,2,3] = [1,2,3] + []
     * [] + [] = [] = [] + []
     */
    identity(empty, ele, operation) {
        return operation(empty, ele) === ele
    }
}

和其他代数结构一样，幺半群同样存在到其他代数结构的同态态射：

/**
 * 数值列表幺半群 与 数值加法幺半群 的同态态射
 * sum ::: [Int] ->- Int 
 */
export type sum = (a: List<number>) => number
export const sum: sum = (a: List<number>): number => {
    return a.reduce((acc, cur) => acc + cur, 0)
}

代数结构可以通过彼此间的组合构成新的代数结构。例如，两个幺半群可以组合构成元组（tuple），此时元组也是一个幺半群：

/**
 * tuple monoid，元组幺半群
 * 这是一种组合两种幺半群的构造方法。
 */
export type TupleMonoid<M1,M2> = Monoid<[M1,M2]>
export const TupleMonoid = <M1,M2>(m1:Monoid<M1>,m2:Monoid<M2>):TupleMonoid<M1,M2> => {
    return {
        biOperation: ([a1,a2],[b1,b2]) => [m1.biOperation(a1,b1),m2.biOperation(a2,b2)],
        empty: [m1.empty,m2.empty],
        identity: (empty,ele,operation) => {
            return operation(empty,ele) === ele
        },
        associative: (a,b,operation) => {
            return operation(operation(a,b),b) === operation(a,operation(b,a))
        }
    }
}
export const exampleTupleMonoid = TupleMonoid(MonoidNumberWithAddition,MonoidNumberWithMultiplication)

好吧，做个简短的总结

这篇 Blog 主要集中于介绍三个基本的代数结构：原群、半群与幺半群。我们通过递进地定义诠释了各个代数结构的定义与相关的特性。

代数结构的意义在于为我们提供了一种理解数据结构的视角，数据本身可以被视为某种代数结构，数据之间的变换可以理解为不同代数结构间的态射。

对于我们熟知的对象，则可以把它看作是某种代数结构对于一个数值集合的作用。

事实上这篇文章只是满足我个人的抽象瘾写的一篇，只是一些概念的罗列以及使用Typescript进行描述。真正要深入到FP还要讲很多东西。但我不清楚接下来我有没有空把它们写出来。

Reference

[1]: Functional Programming with Abstract Algebra Day1.Tom Schrijvers.嗯，很可惜我因为没有版权木得给出链接

【END】