【Translation】改译 | 不确定性计算器
"对 Filip Hráček 的博文 Unsure Calculator 的改译。"
这是对于 Filip Hráček 的博文 Unsure Calculator 的翻译。 这篇博文非常有意思,能够让我们去思考对于不确定性的数值化辅助决策,作者的不确定性计算器在我看来非常实用且好玩。 部分内容根据个人喜好做了改译。内容有删节。
对于原作者撰写的不确定性计算器的示例,可前往原作者的 Blog 查看:https://filiph.github.io/unsure/。

计算你不确定的数字
嗨,我是 Filip,我想向你介绍一个早期版本的不确定性计算器 (uncertainty calculator)。
我们往往借助统计数据(statistics)去衡量现实中的不确定性。统计数据看似吓人,但实际上并非如此。简而言之,统计学本质上就是在表达: 我对这些数字并不确定,但仍想从中进行推理。 事实上,我们生活中对许多事都难以确定,但显然,面对现实我们不能就此束手无策地说 “哎,我又不是统计学家” ,而后将它置之不理。
因此,在这里,我想要介绍我关于我的不确定性计算器以及相应符号的设计。
我设计的不完美的不确定性符号(imperfect uncertainty notation)
其理念很简单:除了常规数字(如 4、3.14 或 43942)外,你还可以输入 范围值 (如 4~6、3.1~3.2 或 40000~45000)。我们使用 ~ 用于分隔 范围 两端极值。你可以在大多数键盘上都能找到它,但为了方便起见,我也在上方的计算器的的虚拟键盘中也包含了该符号。
我们管 ~ 叫做 范围标记(range notation)。
范围标记 向计算器传达了以下信息: 我不确定这里的精确数值,但我有 95%的把握它位于这个范围内。
我经过长时间的深思熟虑,最终得出结论:简洁是关键。是的,我们本可以为不同的概率分布、置信水平、截断处理、协方差等等设计各种符号标记。但那样做反而会增加理解的难度。
我的假设是,如果你已经对置信水平这类概念驾轻就熟,那你可能更倾向于使用更复杂的工具。而在这里,我们的目标是向广大读者揭开统计学的力量。
阅读标记很简单:当你看到 10~15 时,应该说:"十到十五"。
大多数人眼里的统计数据
人们在遇到不确定性时会短路。"嗯,这个不确定,那个也不确定,所以无所谓。"
“嗯,我不确定这个具体数字,所以我就选一个看起来合理的第一个数字来算吧。”
请不要这样!我们的大脑喜欢简单的数字、直接的答案,但这其实是个陷阱。请看下文。
一个实际例子
这个例子源自一个真实的故事。
那是2015年,我们家面临着一个两难选择。一方面,我有机会申请去世界另一端工作,妻子和我都认为换个地方生活几年会是很棒的体验,也欢迎这个学习机会;但另一方面,我们在城里的小公寓刚办完新的按揭贷款,还有个一岁大的宝宝。
我想至少了解一下这在财务上是否是个好举措。如果我选择换个地方生活,我们会亏钱吗?如果会,速度有多快
问题是,一切都不确定。公司在我们完成大部分流程后 才会告知薪资。我向朋友和网上的陌生人打听当地生活成本,得到的数字却天差地别。甚至连税率都不是简单的百分比,而是“视情况而定”。
起初,我用一个简单的电子表格进行计算。我为每个变量选取了一个相对保守的数字并进行计算。1500 美元(650)房租,150 美元(30)婴儿用品,20 美元($20)交通费:
1500 * 0.6 - 650 - 150 - 30 - 20 = 50看起来我们每月能多赚50美元,但它的前提是不花任何额外的钱。一方面,这很酷:我们搬家不是为了发财;另一方面,这有点吓人。如果我在某些数字上不够保守,等意识到时已经让家庭破产了怎么办?
我的意思是说,知道一个潜在结果 (one potential result) 是每月+50 美元固然不错。但其他可能的结果呢?
有一则捷克喜剧戏剧中的独白我相当喜欢,它的台词大概是:“根据我们的碳年代测定分析,这封信写于1842年1月21日,正负两千年。”
很好😼,这便是不确定性计算器大展身手的地方了!
先前,我们的这个小小的公式里其实有不少值实际上是范围值(ranges)。虽然不确定具体数值,但我确实很清楚每个值大致会落在哪个区间内。
让我们用范围重新计算一下:
1400~1700 * 0.55~0.65 - 600~700 - 100~200 - 30 - 20 = -60~220现在,我有95%的把握确定每项物品的真实价值都在这个范围内。也就是说,我同样有95%的把握认为真实余额将落在-60美元至+220美元的区间内。这比之前单一的数字要有用得多。首先,我现在知道我们很有可能会亏损。
我也有概率分布和百分位数:
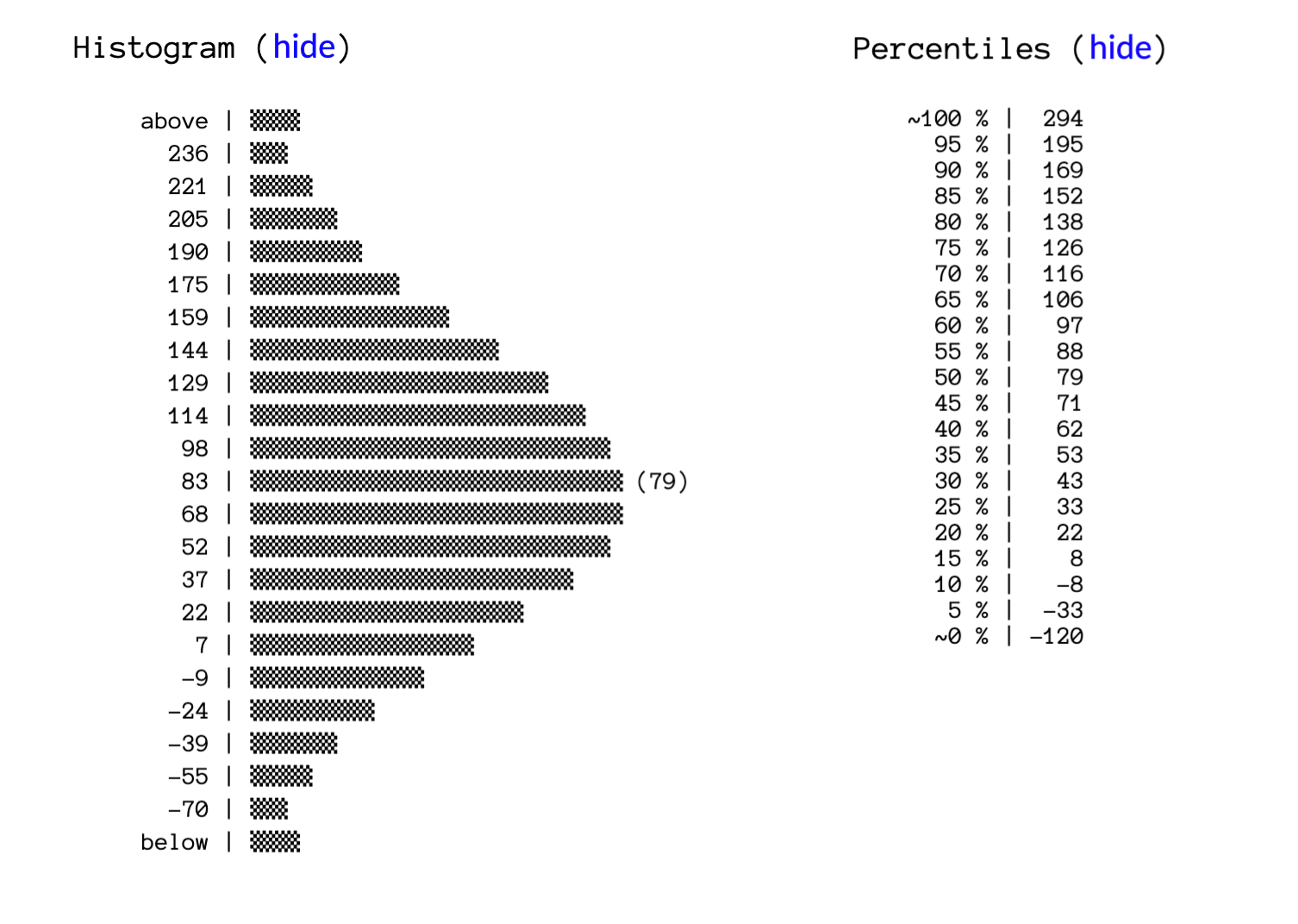
百分位数显示,我们的月度收支有10%的概率会达到-8美元或更糟。(因为-8美元对应的是第10百分位数,意味着10%的结果会比-8美元更低,反之则有90%的结果会高于-8美元。)现在,我们家能做出更明智的决定了:我们是否愿意承受因这一变动导致10%的亏损风险?又是否能接受每月损失33美元或更多的5%概率风险?
这个问题的答案取决于家庭和具体情况。没有孩子和房贷时,我比现在更容易冒险。另一方面,如果我们没有备用计划,我会对10%的风险机会更加谨慎。
最后,我们做到了。而且,在我们的情况下,它恰好得到了回报。结束。
一个科幻示例(sci-fi example)
不确定性计算器专为实用、日常计算而设计。前一节便是一个应用实例。不过,我可不想错过……用外星人来举例的机会。
天体物理学中有一个著名公式叫德雷克方程 (Drake equation),它是对银河系内可能与之交流的文明数量的估算。
例如,如果我们接收来自恒星的无线电信号,是否应该预期银河系中有数百个文明正试图相互联系?还是更像数千个?或者为零?期待我们是孤独的存在是否现实?
德雷克方程 (Drake equation) 其实非常简单:它只是 7 个数字的乘积:
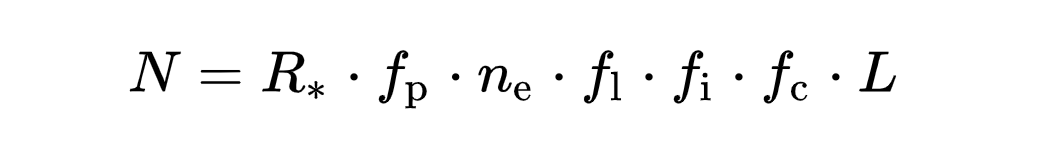
最初由弗兰克·德雷克(Frank Drake)于 1961 年提出的公式及其参数如下:银河系中每年形成一颗恒星(R*),其中五分之一(fp)拥有约 3 颗行星(ne),这些行星中 100%(fl)最终会孕育生命,其中 100%(fi)会演化出智慧生命,再其中有 10%(fc)能发展出通信能力,并持续存在 100 万年(L)。
如果你把这些数字加起来,会得到 60,000 这个数字。在任何时候,都应该有 6 万个文明试图在银河系中相互交流。它们在哪里?
正如你所料,自1961年以来,关于这个方程式的讨论一直很多。不同天体物理学家对每个参数的估计值差异极大。
那么,我们来获取最新估算值,并将其放入 范围 中。结果如下:
1.5~3 x 0.9~1.0 x 0.1~0.4 x 0.1~1.0 x 0.1~1.0 x 0.1~0.2 x 304~10000如果我们把它输入到不确定性计算器中,会得到这个结果:
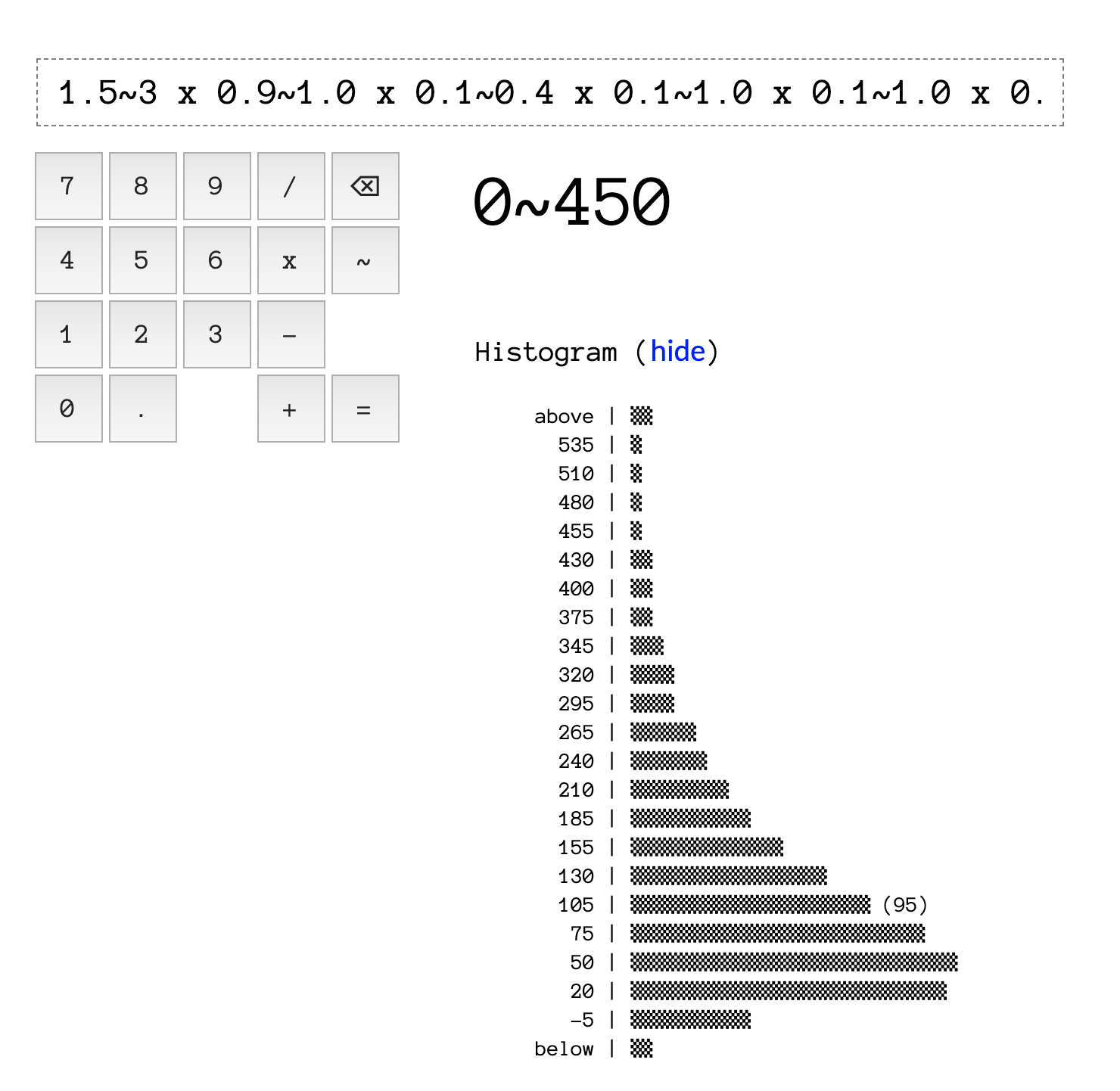
因此,我们预计文明的数量可能在0到450个之间。而概率倾向于较低的一端(直方图在底部更宽)。
NOTE:如果你好奇为什么直方图中会出现负数(
-5),这只是“不确定计算器” (Unsure Calculator) 因设计简洁性而不可避免的缺陷。在缺乏更多信息的情况下,该计算器无法判定负数是否合理(例如,你不可能拥有-5 个文明)。
其他用例
以下是一些关于如何使用此计算器及其符号的建议:
- 评估一个商业想法的可行性,存在不确定的市场规模、不确定的市场份额、不确定的人均月销售额以及不确定的运营成本。例如:
50000~80000 x 0.10~0.20 x 5~10 - 20000~50000 - 估算未来收入,考虑每月不确定的金额、零工时长和税率。例如:
1000~1500 x 10~12 x (30~50 / 100) - 估算洗碗机(或任何其他技术设备)节省的时间,考虑每周使用次数不确定、每次使用节省时间不确定、使用寿命不确定及安装成本不确定。例如:
(3~5 * 5~10 * 51 * 7~15) / 60 - 10~15 - 估算投资账户的总回报。利率和投资期限均不确定。例如:
5000 x (-2~5 / 100) x 5~10 - 估计在疫情中死亡的概率,给定不确定的发病率(多少人会生病)和死亡率(多少感染者会死亡)。例如:
(10~30 / 100) * (0.1~1.0 / 100) * 100 - 估计一座摩天大楼的高度,给定一个不确定的基座距离,以及我们看到其顶部时的不确定角度。例如:
100 x tan(70 ~ 80) - 估算营销活动的投资回报率 (return on investment),考虑不确定的展示量 (views)、不确定的点击率 (click through rate)、不确定的转化率 (conversion rate) 以及不确定的支出 (spend)。例如:
1000000 x (2~3 / 100) x (3~5 / 100) x (10~15)
关于网页上可用的不确定性计算器的缺点
这是我自娱自乐的产物,你应该预料到在最上方提供的不确定性计算器的缺点。它的公式解析器 (formula parser) 很脆弱,给出的错误信息也没什么帮助。
它的计算过程相当缓慢。为了尽可能保持灵活性,我使用了蒙特卡洛方法 (Monte Carlo method)。这意味着计算器对你提出的每个运算都要执行约 25 万次基于 AST 的计算。
这个 UI 说难听点很丑。
共享公式的唯一方法是手动构建 URL。例如,将某人引导至 https://filiph.github.io/unsure/#f=20~30 将自动为其计算 20~30。
范围将始终呈正态分布,下限值为均值减去两个标准差,上限值为均值加上两个标准差。就输入概率分布而言,无法实现更复杂的设定。
当然,这不是统计学家的工具。不确定性计算器适用于快速估算。如需更复杂的计算,请使用免费或付费的统计工具、完整的编程环境,或者聘请统计学家。
我希望一些人会觉得这个工具有用,尽管它有局限且设计简陋。
P.S.: 如果你想帮助改进此工具,或想获取命令行版本,请访问 github.com/filiph/unsure。
【END】